Mathematik trifft Ästhetik
Forscher der Freien Universität Berlin entschlüsseln den Nutzen schöner geometrischer Flächenfüllungen / Neue Studie verbindet künstlerische Muster mit mathematischer Forschung
Nr. 158/2025 vom 10.10.2025
Mathematiker der Freien Universität Berlin zeigen in einer neuen Studie, wie ebene Kachellungen – also Muster, die aus geometrischen Formen bestehen und eine Fläche lückenlos ohne Überlappungen bedecken – weit mehr sind als kunstvolle Ornamente. Sie dienen zugleich als präzise Werkzeuge zur Lösung komplexer mathematischer Probleme. Die Studie dazu mit dem Titel „Beauty in/of Mathematics: Tessellations and Their Formulas“ von Prof. Dr. Heinrich Begehr und dem Doktoranden Dajiang Wang wurde im renommierten Fachmagazin Applicable Analysis veröffentlicht. Sie verbindet Erkenntnisse aus der komplexen Analysis, der Theorie partieller Differentialgleichungen und geometrischer Funktionentheorie.
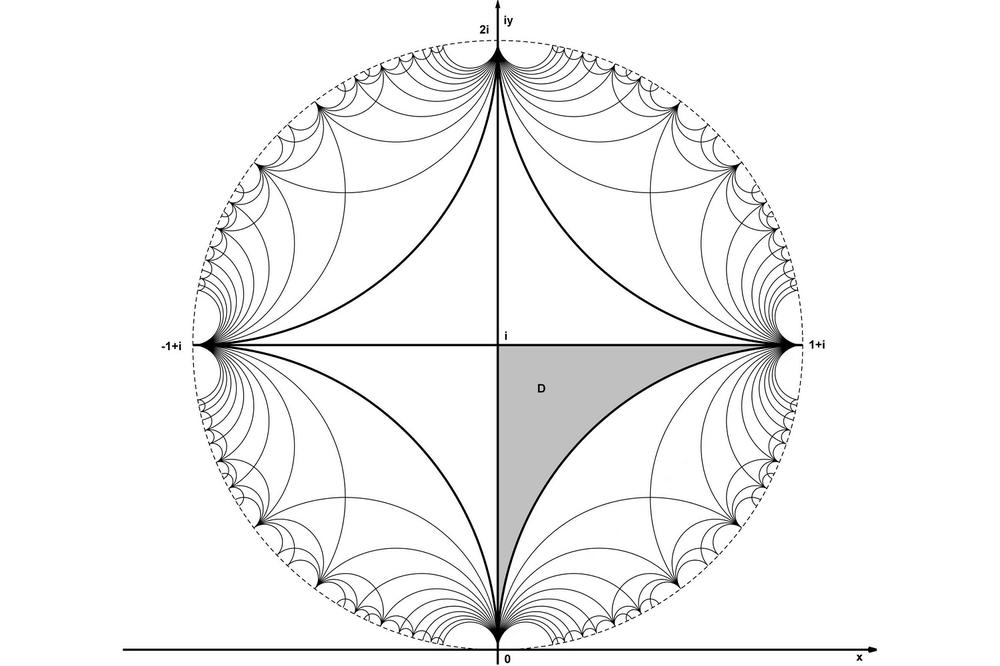
Ästhetik und Mathematik: Die Pflasterung eines Kreises mithilfe des Schweikart-Dreiecks.
Bildquelle: Heinrich Begehr
Im Mittelpunkt der Arbeit steht das sogenannte Parqueting-Reflection-Prinzip: Durch sukzessive Spiegelungen an geraden Linien und Kreisen entstehen hochsymmetrische Muster, wie man sie aus den kunstvollen Werken von M.C. Escher kennt. Sie dienen als Grundlage zur Lösung klassischer Randwertprobleme der Mathematik – etwa des Dirichlet- oder Neumann-Problems.
„Unsere Forschung zeigt, dass Schönheit in der Mathematik nicht nur durch Ästhetik auf die Sinne wirkt, sondern mit Effizienz und struktureller Tiefe verbunden ist“, erklärt der Mathematiker Prof. Dr. Heinrich Begehr. „Während sich bisherige Untersuchungen zu Kachellungen auf die Art von Pflasterungen der Ebene und des Raumes beziehen, an der sich auch der Nobelpreisträger Roger Penrose beteiligt hat, ermöglicht die Spiegel-Kachel-Methode, Darstellungen von Funktionen in den Gebieten der Kachellungen zu entwickeln, die für Anwendungen in mathematischer Physik und Technik brauchbar erscheinen.“
Es werden konkrete Formeln für Kernfunktionen – darunter Green-, Neumann- und Schwarz-Kerne – aus den geometrischen Spiegelungsmustern hergeleitet. Damit gelingt ein eleganter Brückenschlag zwischen geometrischer Intuition und analytischer Präzision.
Seit über einem Jahrzehnt hat die Methode viele Anwender gefunden, unter ihnen viele junge Wissenschaftler. An der Freien Universität Berlin sind einschließlich der Entstehungsphase der Methode 15 Dissertationen und Diplomarbeiten beteiligt, 7 Dissertationen sind im Ausland dazu gekommen.
Besonders bemerkenswert: Die Methode funktioniert nicht nur im euklidischen Raum, sondern auch in hyperbolischen Geometrien, wie sie in der theoretischen Physik oder modernen Visualisierungen der Raumzeit verwendet werden. Hierzu hatte Begehr bereits im vergangenen Jahr eine weitere Arbeit „Hyperbolic tessellation: Harmonic Green function for a Schweikart triangle in hyperbolic geometry“ in der Zeitschrift Complex Variables and. Elliptic Equations veröffentlicht.
„Wir hoffen, dass unsere Ergebnisse sowohl in der reinen Mathematik als auch in der mathematischen Physik Anklang finden – und vielleicht sogar in der Architektur oder Computergrafik inspirieren“, ergänzt Dajiang Wang.
Berliner Spiegel-Kacheln: Mathematik mit Tradition
Bereits seit rund zwei Jahrzehnten erforscht die Arbeitsgruppe um Heinrich Begehr am Institut für Mathematik der Freien Universität Berlin die sogenannten Berliner Spiegel-Kachellungen – ein Verfahren, das auf dem einheitlichen Spiegelungsprinzip des Berliner Mathematikers Hermann Amandus Schwarz (1843–1921) basiert.
Dabei wird ein Kreispolygon – eine Fläche mit Rändern aus Geraden- und Kreisbögen – durch wiederholte Spiegelung so oft abgebildet, bis die gesamte Ebene überdeckungsfrei lückenlos ausgefüllt ist. Diese Muster entstehen nicht nur als optisch faszinierende Strukturen, sondern ermöglichen auch explizite Integraldarstellungen von Funktionen – ein zentraler Kern zur Lösung komplexer Randwertprobleme.
„Was einst beim Blick in einen dreiteiligen Frisierspiegel eine unendliche Bildfolge erzeugte, entsteht heute mit iterativen Computerprogrammen und wir ergänzen diese durch exakte mathematische Formeln für die komplexe Analysis“, erklärt Begehr.
Schweikart-Dreiecke und hyperbolische Schönheit
Besonders herausfordernd und zugleich ästhetisch eindrucksvoll sind Parkettierungen in hyperbolischen Räumen – etwa innerhalb einer Kreisscheibe. Hier kommen sogenannte Schweikart-Dreiecke zum Einsatz: spezielle Dreiecke mit einem rechten und zwei Nullwinkeln, benannt nach dem Hobbymathematiker und Juraprofessor Ferdinand Kurt Schweikart (1780–1857).
Diese Dreiecke ermöglichen eine vollständige, regelmäßige Parkettierung der Kreisscheibe – mit einer Ästhetik, die auch Computergrafikern und Architekturschaffenden neue Inspiration bietet. Gleichzeitig sind die zugrunde liegenden mathematischen Konstruktionen hochkomplex und erfordern tiefe analytische Methoden.
Mathematik als visuelle Wissenschaft
Die Ergebnisse der neuen Studie des Berliner Forschungsteams verdeutlichen eindrucksvoll: Mathematik ist nicht nur eine abstrakte Disziplin – sie ist auch eine visuelle Wissenschaft, in der Ordnung, Symmetrie und Ästhetik eine tragende Rolle spielen. Besonders in Verbindung mit moderner Visualisierung, Grafiksoftware und digitalen Anwendungen gewinnen die Erkenntnisse zusätzlich an Relevanz.
Weitere Informationen
- Die Studie: Heinrich Begehr, Dajiang Wang: „Beauty in/of Mathematics: Tessellations and Their Formulas“, ist online abrufbar: https://www.tandfonline.com/doi/full/10.1080/00036811.2025.2510472#d1e153
- Die Studie: Heinrich Begehr: “Hyperbolic tessellation: Harmonic Green function for a Schweikart triangle in hyperbolic geometry”, ist online abrufbar: https://doi.org/10.1080/17476933.2024.2408729
Kontakt
- Prof. Dr. Heinrich Begehr, Freie Universität Berlin, Institut für Mathematik, E-Mail: heinrich.begehr@fu-berlin.de
- Dajiang Wang, Freie Universität Berlin, Institut für Mathematik, E-Mail: wang1996jiang2022@163.com