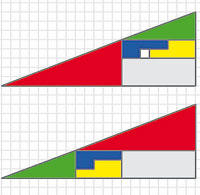
Wo bitte ist das kleine weiße Feld geblieben?
Bei dieser Knobelaufgabe kommen sogar Geometrie-Fans ins Grübeln
Es gibt Sachen, da traut man seinen Augen kaum. Dinge, die eben noch da waren, sind plötzlich wie vom Erdboden verschwunden. Magie oder höhere Mathematik? Das ist auch die Frage bei der aktuellen Knobelaufgabe, die Ihnen Professor Ehrhard Behrends von der Freien Universität Berlin in dieser Beilage stellt. Und so lautet sie:
Wenn man in einem aus verschiedenfarbigen Feldern zusammengesetzten Dreieck die Teile umsortiert, verschwindet plötzlich ein Feld. Das kann doch nicht sein, oder? Wo bitte ist das weiße Quadrat geblieben?
Sollten Sie des Rätsels Lösung haben, schreiben Sie sie bitte auf eine Postkarte und schicken sie an folgende Adresse: Freie Universität Berlin, Kommunikations- und Informationsstelle, Stichwort: Mathematikaufgabe, Kaiserswerther Straße 16 – 18, 14195 Berlin. Und bitte nicht vergessen, Ihren Absender gut lesbar auf der Karte anzugeben und eine Telefonnummer, unter der wir Sie erreichen können. Einsendeschluss ist der 1. Oktober 2008.
Dieses Mal machen wir Ihnen das Mitspielen besonders schmackhaft. Zu gewinnen gibt es zwei Essensgutscheine zu je 50 Euro im italienischen Restaurant „Galileo“ über den Dächern der Freien Universität Berlin. Wir drücken Ihnen die Daumen!
Um Wohlschmeckendes – genauer gesagt um Süßes – ging es auch in unserer letzten Aufgabe in der Juli-Beilage. Und mit Süßem kennen sich unsere Leser offenbar bestens aus. Wie viele Handgriffe braucht man mindestens, um eine Tafel Schokolade mit fünf Reihen zu je zwölf Feldern so zu zerbrechen, dass man am Ende die Einzelstücke erhält? Das wollten wir von Ihnen wissen.
Die richtige Lösung erreichte uns auf zahlreichen Postkarten und Briefen und lautet: Die Tafel muss 59 Mal gebrochen werden. Die mathematische Begründung ist überraschend einfach. Am Anfang hat man ein Stück, und – egal, wie weit man gekommen ist – durch Zerbrechen von einem Teilstück erhöht sich die gerade erreichte Anzahl um ein Stück. Um also die 60 Einzelstücke zu erhalten, sind 59 Handgriffe erforderlich. Die Versuchung ist groß, an dieser Stelle ein Loblied auf die Mathematik zu singen. Wenn man nämlich die Begründung verstanden hat, so sieht man, dass es von der konkreten Schokolade nicht abhängt. Statt 5 mal 12 Felder hätten es auch 10 mal 200 Felder sein können (oder noch viel, viel mehr): Um die 10 mal 200, also die 2000 Einzelstücke zu erzeugen, sind auf jeden Fall 1999 Bruchvorgänge notwendig.
Um den Aufwand zum Vergleich bei einem „Computerbeweis“ zu veranschaulichen, betrachten wir noch einmal das 5-mal-12-Felder-Problem. Es gibt etwa 263 Billionen verschiedene Möglichkeiten, die Tafel in Einzelstücke zu zerbrechen, und wenn unser Supercomputer pro Sekunde eine Million Möglichkeiten nachprüft, hat er etwa 3048 Tage – also etwas mehr als acht Jahre – damit zu tun, sie alle auf die bestmögliche Variante zu prüfen. Für die 10mal200-Tafel würden selbst die schnellsten Rechner schlappmachen, denn das Nachprüfen aller Möglichkeiten würde sie mehr Stunden beschäftigen, als seit dem Urknall vergangen sind.
Unter den richtigen Einsendern darf sich Wolfgang Schmitt aus Berlin-Steglitz besonders freuen. Er wurde als Gewinner unseres Rätsel-Preises gezogen und erhält den dekorativen Gipsabguss eines weiblichen Kykladen-Idols aus der Abguss-Sammlung Antiker Plastik des Instituts für Klassische Archäologie der Freien Universität Berlin. FU