Neue Knobelaufgabe fordert Denker und Tüftler heraus

So leicht kann unseren Lesern niemand etwas vormachen. Sie kennen sich mit Wahrscheinlichkeitsrechnung aus. Das zeigen die vielen richtigen Einsendungen zu unserer Knobelaufgabe in der Aprilausgabe der Beilage der Freien Universität, die uns in den vergangenen Wochen erreicht haben. Noch einmal zur Erinnerung. Es ging um ein Spiel auf dem Abschlussball einer Tanzschule. Wir hatten gefragt, wie groß die Wahrscheinlichkeit ist, dass bei einer zufälligen Auslosung mindestens einmal das „richtige“ Paar zusammenkommt. Und die Wahrscheinlichkeit dafür ist überraschend hoch: Sie liegt bei etwa 63 Prozent. Deswegen war „c“ die richtige Antwort.

Um das Ergebnis zu verstehen, muss man „nur“ richtig zählen können. Bei n Paaren gibt es 1 mal 2 mal … mal n Möglichkeiten der Anordnungen, Mathematiker schreiben dafür „n!“ und sagen „n Fakultät“. Bei wie vielen dieser Situationen hat sich mindestens ein Paar wiedergefunden?

Betrachten wir etwa Paar 1. Dass dieses zusammenkommt, wird in (n–1)! Fällen passieren, auf so viele Weisen nämlich kann man die restlichen Paare anordnen. Für die anderen Paare geht die Rechnung genauso, und – naiv betrachtet – würde man nun die Antworten addieren. Doch halt: Manche Situationen sind mehrfach gezählt, zum Beispiel die, wo sich alle Paare wiedergefunden haben.

Um zur richtigen Anzahl zu kommen, muss man also noch etwas genauer hinsehen. (Das ist so ähnlich, als wenn man weiß, dass in einem Bus 16 Frauen und 7 Bayern sitzen. Um die Gesamtzahl der Passagiere richtig zu ermitteln, muss man noch berücksichtigen, wie viele bayerische Frauen dabei sind. Sind das zum Beispiel 5, so lautet das richtige Ergebnis 16 + 7 – 5, also 18.) Am Ende ist die richtige Wahrscheinlichkeit durch den Wert 1– 1/2! + 1/3! –± 1/n! gegeben, und das stimmt recht genau mit 1-e^-1 überein. Hier ist e die Eulersche Zahl, und man muss sich an die e-Reihe erinnern. So kommt die Wahrscheinlichkeit von 0,63 zustande.

Von den Rechenassen, die die richtige Lösung gefunden haben, dürfen sich fünf am 14. Juni zur Langen Nacht der Wissenschaften einen schönen Abend machen: Sie haben eine Familienkarte gewonnen und damit freien Eintritt für sich, ihre Ehepartner und die Kinder. Gewinner sind: Christine Dalkowski, Hans Jäh, Laura Geßmann von Kersbergen, Charlotte Kern und Winfried Rönsch. Herzlichen Glückwunsch!

Auch bei der neuen Aufgabe, die wieder aus der Feder von Mathematik-Professor Ehrhard Behrends stammt, lohnt sich das Mitmachen: Zu gewinnen gibt es fünf Mal je zwei Eintrittskarten für den Botanischen Garten und das Botanische Museum. Der Garten ist zu allen Jahreszeiten einen Besuch wert. Zuvor müssen Sie aber die kleinen grauen Zellen arbeiten lassen.

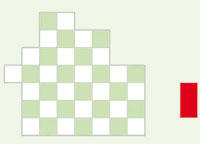
Diesmal knobeln wir mit einem leicht lädierten Schachspiel mit grünen und weißen Feldern. Dazu gibt es rote Spielsteine in beliebiger Anzahl: Jeder Spielstein ist genauso groß, dass er zwei Felder des Schachspiels abdeckt. Die Frage lautet: Kann man das Schachspiel mit den roten Steinen lückenlos so bedecken, dass sich nirgendwo zwei rote Steine überlappen?

Falls Sie eine Lösung haben, schicken Sie bitte eine Skizze ein. Falls Sie meinen, dass das nicht geht, hätten wir gern eine Begründung.

Die Auflösung schicken Sie bitte an folgende Adresse: Freie Universität Berlin, Kommunikations- und Informationsstelle, Stichwort: Mathematikaufgabe, Kaiserswerther Straße 16–18, 14195 Berlin.

Und bitte vergessen Sie nicht, Ihren Absender gut leserlich! auf der Karte anzugeben und eine Telefonnummer, unter der wir Sie erreichen können. Einsendeschluss ist der 1. Juli. Wir drücken Ihnen die Daumen!