Rechnen hilft!
Wie die Mathematik die Medizin voranbringt
22.10.2012
Wie funktioniert das Leben auf molekularer Ebene? Warum werden Menschen krank, und wie lässt sich das verhindern? Wissenschaftler des DFG-Forschungszentrums MATHEON nutzen hoch komplexe Modelle, um Antworten auf diese Fragen zu finden.
Bildquelle: photocase, brombeerblatt http://www.photocase.de/foto/17904-stock-photo-dinge-gesundheitswesen-medikament-verpackung
Wie funktioniert das Leben auf molekularer Ebene? Warum werden Menschen krank, und wie lässt sich das verhindern? Wissenschaftler des DFG-Forschungszentrums MATHEON nutzen hoch komplexe Modelle, um Antworten auf diese Fragen zu finden. Mithilfe von mathematischen Methoden können neue Behandlungsansätze auf molekularer Ebene simuliert und unterschiedliche Therapieschemata verglichen werden. Das ersetzt zwar nicht den klinischen „Praxistest“. Es kann aber zu einem sehr viel rationaleren Vorgehen bei der Etablierung neuer Behandlungskonzepte beitragen.
Virtuelle Modelle erstellen, bestimmte Rahmenbedingungen am Computer simulieren, das Modell optimieren, erneut simulieren: Nach diesem letztlich immer gleichen Schema läuft heute die Entwicklung zahlloser Innovationen in den unterschiedlichsten Bereichen ab. Egal ob der Verbrauch eines Autos verringert, eine Staumauer gebaut oder ein neues Flugzeug entworfen werden soll; immer werden mögliche Szenarien mithilfe mathematischer Modelle und unter Berücksichtigung möglichst vieler relevanter Einflussfaktoren erst einmal durchgerechnet, bevor es fertige Produkte gibt, die sich anfassen lassen. „Trial and error“ wäre in vielen derartigen Entwicklungssituationen viel zu kostspielig, teilweise auch gefährlich.
In der Medizin erinnert die Entwicklung neuer Behandlungsansätze dagegen heute noch immer häufig an „Trial and Error“. Zwar werden Arzneimittel für die Therapieforschung mittlerweile in der Regel auf Basis molekularer Erkenntnisse ausgewählt. Das komplexe Zusammenspiel zwischen unterschiedlichsten molekularen Faktoren wird dabei aber oft nicht ausreichend berücksichtigt. Stattdessen werden relativ rasch Tierversuche oder auch klinischen Studien durchgeführt. Unzählige dieser Studien scheitern, und oft verstehen die Experten erst viel später, warum ein bestimmter Ansatz nicht funktionierte, vielleicht von Anfang an gar nicht funktionieren konnte.
Simulation auf der Ebene von Molekülen
Die Mathematik kann einen Beitrag zur Optimierung der molekularen und der klinischen Forschung leisten, sagt Professor Dr. Christof Schütte, Co-Chair des DFG Forschungszentrums MATHEON und Leiter der Biocomputing Group an der Freien Universität Berlin: „Letztlich versuchen wir, mithilfe des Biocomputings die Erfolgsgeschichte der mathematischen Modellierung in vielen anderen Disziplinen auch im molekularbiologischen beziehungsweise systembiologischen Kontext zu replizieren“, sagt Schütte. Auf Basis möglichst umfangreicher Detailinformationen zu Wirkstoffen, Krankheitserregern oder molekularen Gegebenheiten auf Patientenseite werden von den Biocomputing-Experten anwendungsnahe Modelle erstellt und Algorithmen formuliert. Damit lässt sich in einem zweiten Schritt simulieren, was passiert, wenn beispielsweise in einem Gewebe bestimmte Umgebungsparameter beeinflusst werden, oder wenn bei einem Medikament einfach nur die Behandlungsfrequenz verändert wird.
Wie das konkret aussehen kann, haben Schütte und seine Kollegen in den vergangenen Jahren sehr detailliert am Beispiel der HIV-Infektion vorgemacht. „Diese Erkrankung eignet sich deswegen gut für die mathematische Modellierung, weil über ihre molekularen Details vergleichsweise viel bekannt ist“, sagt Dr. Max von Kleist, Nachwuchsgruppenleiter Biocomputing am MATHEON. HIV lässt sich in den Industrienationen mithilfe aufwendiger Kombinationstherapien und regelmäßiger Resistenzdiagnostik gut in Schach halten. Gelöst ist das globale HIV-Problem dadurch aber noch lange nicht. Zum einen besteht nach wie vor ein erheblicher Bedarf an Diagnose- und Therapiekonzepten, die auch in armen Ländern mit schlechter Infrastruktur funktionieren. Zum anderen haben weder Entwicklungs- noch Industrieländer bisher das Problem der Virusübertragung zufriedenstellend im Griff, sodass immer wieder neue, auch arzneimittelbasierte Präventionskonzepte diskutiert werden.
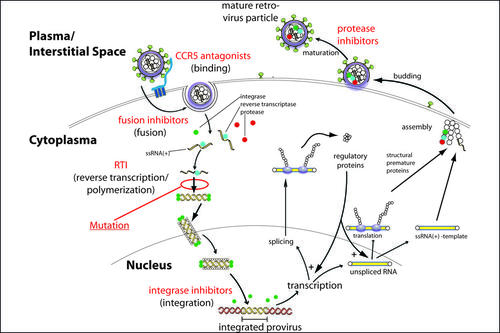
Der Lebenszyklus eines HI-Virus: Die Abbildung zeigt die unterschiedlichen Stadien des HI-Virus und die Inhibition der unterschiedlichen Stadien durch verschiedene Wirkstoffklassen.
Bildquelle: Max von Kleist
Einmalpille für Sex ohne Reue?
Diese arzneimittelbasierte Prävention haben sich von Kleist und seine Kollegen in letzter Zeit etwas genauer angesehen. Ein unter HIV-Experten kontrovers diskutierter Ansatz, um eine Virusübertragung zu verhindern, ist die sogenannte Präexpositionsprophylaxe, kurz PrEP genannt. Dabei werden Menschen, die zwar nicht mit HIV infiziert sind, aber ein hohes Infektionsrisiko aufweisen, mit einem antiretroviralen Medikament behandelt, einem Medikament also, das sonst für die Behandlung von HIV-Infizierten eingesetzt wird. Risikopersonen, die für eine PrEP prinzipiell in Frage kommen, sind beispielsweise die Partner von HIV-infizierten Menschen, aber auch Menschen mit häufigen wechselnden Sexualkontakten in stark HIV-gefährdeten Milieus.
„Mathematisch interessant an dieser Thematik ist die Frage, ob eine solche Prophylaxe bei allem, was wir über das Virus und über die in Frage kommenden Medikamente wissen, überhaupt hinreichend effektiv sein kann“, erklärt von Kleist. Vor allem wollten die Wissenschaftler wissen, wie abhängig die Effektivität einer „PrEP“ vom Einnahme-Intervall der Medikamente ist. Um das zu klären, wurde am Beispiel des in der HIVTherapie sehr weit verbreiteten Medikaments Tenofovir ein Wahrscheinlichkeitsmodell entwickelt, in das pharmakologische Eigenschaften des Medikaments ebenso einflossen wie Daten zum Virus und zur Virusexposition.
„Tenofovir wird intrazellulär aktiviert. Damit bauen sich die Wirkspiegel relativ langsam auf. Was wir anhand unseres Modells zeigen können ist, dass eine PrEP mit Tenofovir als Monotherapie sehr ineffektiv ist, wenn das Medikament nur bedarfsweise eingenommen wird“, betont von Kleist. Mit anderen Worten: Eine Pille Tenofovir vor der Party am Abend ist aus mathematischer Sicht definitiv keine sinnvolle Präventionsstrategie. Wird das Präparat täglich eingenommen, steigt die Schutzwirkung. „Aber selbst dann wird nur ein Schutz von etwa 80 Prozent erreicht“, sagt von Kleist. Diese Zahl gilt zudem auch nur, wenn die Genitalschleimhaut intakt ist. Liegen noch andere Infektionserkrankungen im Genitalbereich vor, die die Schleimhaut schädigen, ist die Virusexposition bei ungeschütztem Geschlechtsverkehr mit einem HIV-infizierten Menschen wesentlich höher. Der Schutz durch die medikamentöse PrEP sinkt.
Wenige Wochen, nachdem die Berliner Mathematiker die Ergebnisse ihrer Berechnungen in der Fachzeitschrift PLoS ONE veröffentlicht hatten, hat die US-amerikanische Zulassungsbehörde FDA im Juli 2012 zum ersten Mal ein HIV-Medikament auf Basis zweier klinischer Studien für die PrEP zugelassen. Es handelt sich dabei um eine Kombination aus Tenofovir und einer weiteren antiretroviralen Substanz, Emtricitabin. „Prinzipiell könnten wir mit unserem Modell auch die Effektivität dieser Kombination berechnen. Wir sind aber darauf angewiesen, relativ genaue pharmakologische Daten für die Medikamente zu haben, deren Wirkung wir simulieren. Und diese Daten liegen für Emtricitabin leider nicht vor“, so von Kleist.
Trotzdem zeigen die Ergebnisse der Zulassungsstudien, dass die Berliner Mathematiker mit ihrem Modell im Prinzip goldrichtig liegen. Denn auch in diesen Studien lässt die Effektivität der PrEP bei einer nur bedarfsmäßigen Einnahme sehr zu wünschen übrig. Und die PrEP-Studien zeigen in Übereinstimmung mit dem Modell der Berliner Mathematiker auch, dass bei täglicher Einnahme von PrEP-Medikamenten ein zwar deutlich höherer, aber kein 100prozentiger Schutz vor der HIV-Übertragung erreicht wird. Mit anderen Worten: Dadurch, dass mathematische Modellierung und klinische Zulassungsstudien bei der HIV-PrEP parallel liefen, lässt sich jetzt am Beispiel HIV konkret zeigen, dass die mathematische Modellierung eine realistische Einschätzung der klinischen Realität liefert.
Wie lässt sich ein Neugeborenes optimal schützen?
Genau diese Übereinstimmung zwischen klinischer Realität und mathematischem Modell konnte die Arbeitsgruppe um von Kleist auch für ein zweites Szenario demonstrieren, nämlich für die Übertragung von HI-Viren unter der Geburt von einer infizierten Mutter auf das Kind. Für solche Situationen stehen in Industrieländern moderne Kombinationstherapien zur Verfügung, die die HIV-infizierte Mutter ab Mitte der Schwangerschaft einnimmt und die das Kind weitgehend vor einer Übertragung schützen. Das ist in einigen Entwicklungsländern aber zu teuer beziehungsweise trotz oft subventionierter Medikamente aufgrund der vorhandenen Infrastruktur kaum umzusetzen.
Die Berliner Mathematiker haben nun berechnet, dass die kurzfristige Gabe des kostengünstig als Generikum verfügbaren HIV-Medikaments Nevirapin als Monotherapie unmittelbar vor der Geburt im Hinblick auf die Prophylaxe der Übertragung von HI-Viren auf das Kind fast so effektiv sein kann wie die langfristige Kombitherapie. Und genau das wurde mittlerweile in klinischen Studien mit Nevirapin gezeigt. Auch hier gilt also: Ein mathematisches Modell sagt das Ergebnis einer klinischen Studie relativ genau vorher.
Alzheimer: Verhindern, dass Eiweiße falsch gefaltet werden
Am Beispiel der HIV-Therapien lässt sich der Nutzen von Modellerzeugung, Simulation und Optimierung besonders gut verdeutlichen. Medizinisch relevante mathematische Modelle können aber auch in viel früheren Stadien der Therapieentwicklung ansetzen, etwa bei der Funktionsweise von Molekülen. So gibt es beispielsweise einige chronische Erkrankungen, bei denen der menschliche Körper bestimmte Eiweißmoleküle falsch faltet. Diese falsch gefalteten Eiweiße können sich im Gewebe ablagern und dort medizinische Probleme verursachen. Ein Beispiel dafür ist die Alzheimer-Erkrankung. Hier kommt es im Gehirn zu einer Ablagerung von falsch gefaltetem Beta Amyloid. Ein möglicher Therapie- beziehungsweise Präventionsansatz besteht darin, zu verhindern, dass es zu dieser Fehlfaltung des Beta Amyloid kommt. Nur: Wie lässt sich das erreichen?
Hier kann erneut die Mathematik mit Biocomputing-Ansätzen helfen. „Die Faltung von Eiweißmolekülen lässt sich mit mathematischen Modellen genauso präzise beschreiben wie die Entstehung von Mutationen in Krankheitserregern oder wie die Vorgänge bei der Übertragung eines gefährlichen Virus“, so Schütte. Am Beispiel Alzheimer würde in ein solches Modell die genaue Struktur der relevanten Eiweiße eingehen. Berücksichtigt werden müssen außerdem diverse Gewebeparameter, die die Rahmenbedingungen beschreiben, unter denen es im Gehirn zur Fehlfaltung kommt. Am Modell können dann diverse Umgebungsparameter modifiziert werden, um zu verstehen, warum genau es zur Fehlfaltung kommt.
Im nächsten Schritt kann – immer noch anhand des Modells – versucht werden, die Umgebungsparameter innerhalb eines vorgegebenen Rahmens so zu steuern, dass die Wahrscheinlichkeit einer Fehlfaltung möglichst klein wird. Und das wiederum ist hoch interessant für die Arzneimittelentwicklung, weil es einen Ansatzpunkt für eine sehr viel detailliertere Suche nach potenziellen Wirkstoffen liefert.
Pingpong zwischen den Disziplinen
„Entscheidend für den Erfolg von Biocomputing-Projekten im medizinischen Umfeld ist immer die enge Kooperation mit Biologen und Medizinern“, betont Schütte. Mathematische Modelle liefern nur dann realistische Vorhersagen, wenn sie die biologische Realität möglichst genau abbilden. Dazu gehört, dass zu den untersuchten Krankheitserregern oder Molekülen möglichst viele Detailinformationen vorliegen müssen. „Hier sind wir ganz klar auf die Zuarbeit von Biologen, Pharmakologen und Medizinern angewiesen“, betont Schütte. „Umgekehrt müssen natürlich auch wir Mathematiker ständig bereit sein, unsere Modelle zu optimieren, wenn die Kliniker uns sagen, dass sie aus diesen oder jenen Gründen die Realität nicht adäquat abbilden.“ Gelingt dieses Wechselspiel der Disziplinen, dann können mathematische Modelle in den unterschiedlichsten medizinischen Bereichen dabei helfen, einzuschätzen, welche Therapieansätze erfolgversprechend sind und von welchen man besser die Finger lassen sollte. Das nutzt den Wissenschaftlern und Ärzten, aber auch und vor allem den Patientinnen und Patienten.